How To Create Sudoku In Python

Solve Sudoku using Linear Programming (Python — PuLP)

Exploiting the concepts of linear programming to solve a Sudoku puzzle

**SUDOKU+LINEAR PROGRAMMING** (Image Compilation by Author. Sudoku Images — wiki)

Sudoku is a game typically involving the pen, paper, and mind in action together. When you want to give some rest to the pen & the mind, it can be solved with the Sudoku solvers. Here we will try to create one such Sudoku solver.

This article aims at exploiting the concepts of linear programming to solve a Sudoku puzzle. We will start off by refreshing some of the basic theories behind Linear Programming and then implementing the same in Python using the PuLP package.

Here we will be trying to solve two types of sudoku puzzles, the regular sudoku and the diagonal sudoku, which have additional rules on the diagonals of the Sudoku grid. More on it as we progress.

What is Linear Programming?

Linear programming is a constrained optimization model that has 3 major components: objective function, decision variables, and constraints.

Objective Function: An objective function is a linear function whose value needs to be either minimized or maximized based on the problem we are trying to solve.

Decision Variables: These are the output or target variables that decide the final output.

Constraints: Constraints are the restrictions or the limitations put on the decision variables.

The goal of linear programming is to find an optimal set of decision variables for the given objective function with all the constraints applied. The solution could be a feasible solution or an optimal solution.

Feasible Solution: Solution to a linear program that satisfies all the constraints.

Optimal Solution: Solution to a linear program that satisfies all the constraints with the best objective function value (either maximizing or minimizing the objective function)

Linear Programming & Sudoku

**Linear Programming for Sudoku** (Image by Author)

In the case of Sudoku, we need to identify a feasible solution to solve it.

Solving Sudoku using Linear Programming in Python

Here we will be using the PuLP package in Python to solve this linear programming problem.

Steps to solve the Sudoku problem:

Step 1: Define the Linear Programming problem
Step 2: Set the objective function
Step 3: Define the decision variables
Step 4: Set the constraints
Step 5: Solve the Sudoku puzzle
Step 6: Check if an optimal result is found

Step 1: Define the Linear Programming Problem

Step 2: Set the Objective Function

Normally in linear programming, we have an objective function that we try to either maximize or minimize. But in this case, we do not have any objective function. It is more of a feasibility problem, i.e. if the constraints are satisfied then the sudoku is solved.

Hence we set a dummy objective function here as 0.

Step 3: Define the Target Variables or the Decision Variables

Sudoku grid consists of 81 cells (9x9 grid). Each cell can take a value between 1 and 9. If we create a set of boolean decision variables for each of these values, then we get a total of 729 variables (9x9x9).

Since there can be only one value associated with each cell, only one boolean variable of the 9 variables for a cell can be set to true, the remaining should be false. As you will see in the next section, this is ensured with a constraint.

Step 4: Set the Constraints

Generic constraints for Sudoku

The rules for Sudoku need to be set as constraints to solve this problem.
Given that Sudoku is a 9x9 grid, the rules of the game are mentioned here:

Constraint 1: Each cell should be filled with a single value between 1 and 9

Constraint 2: Each row should contain every number from 1 to 9 once

Constraint 3: Each column should contain every number from 1 to 9 once

Constraint 4: Each 3x3 grid, starting from top left, should contain every number from 1 to 9 once

Additional constraints for diagonal Sudoku

There is another version of Sudoku, known as the diagonal Sudoku, where in addition to the above mention generic rules, the following constraint should also be fulfilled.

Constraint 5: Each diagonal should contain every number from 1 to 9 once

Note that this constraint needs to be applied to both the diagonals (top-left to bottom-right corner and top-right to bottom-left corner).

Constraints to initialize the input Sudoku puzzle

Now that the rules of the game are set through the constraints, the next step is to initialize the known values in the puzzle. This is taken from the Sudoku puzzle that we are trying to solve. Fill the prefilled cells as constraints to the LP problem.

With this, all the required constraints to solve the Sudoku are set and we are ready to solve it.

Step 5: Solve the Sudoku Puzzle

Once the objective function, decision variables, and constraints are set, solving the puzzle is as simple as invoking the solve method on the problem variable.

Step 6: Check if an optimal result is found

Once the problem is solved, we can check if an optimal solution has been identified by the algorithm by checking on the status flag.

If the result is 'optimal' then the Linear Programming algorithm has identified a solution with the given constraints. If a solution cannot be found, then it returns the status as 'infeasible'.

TIME TO SOLVE

Wrap the above code into a function so that it can solve any Sudoku passed as input. Given below are a couple of samples where normal sudoku and diagonal sudoku are solved using this solver.

Sudoku 1 — Normal Sudoku

Input

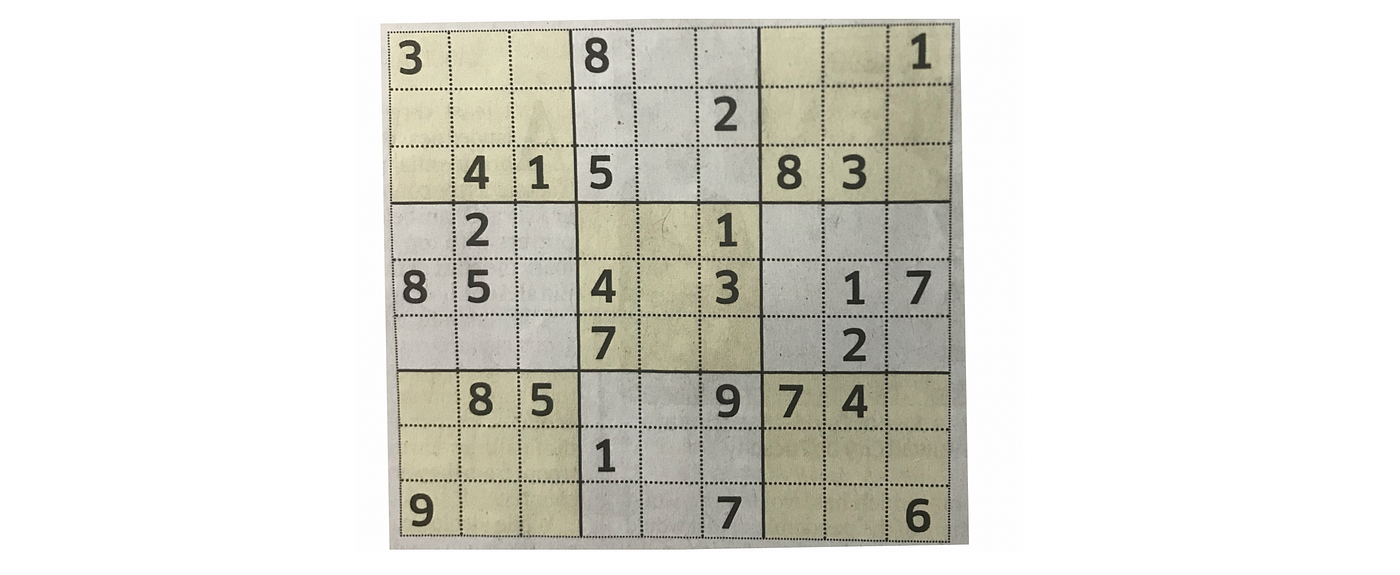
Output

**Solved Sudoku — Normal** (Image by Author)

Sudoku 2 — Diagonal Sudoku

Input

Output

**Solved Sudoku — Diagonal** (Image by Author)

Source Code

Refer to this git repo to get access to the complete code: Sudoku_Solver_LP

Conclusion

This is a very simplistic approach of how the Sudoku puzzle could be solved using the Linear Programming package provided in Python, namely PuLP.

There is scope for further enhancements, like reading the Sudoku grid from an image or video processing to read the grid via the webcam.

More on that later, hope you enjoyed this read!!